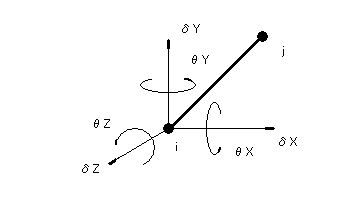|
このページでは、解析モデルの作成に役立つ技術情報を掲載しています。 H2: 面外解析時の支点条件 Frame解析ではX-Y平面上に配置された各節点に対して、下図に示す変位の自由度を考慮しながら解析を進めます。この図は節点iの全自由度(6個)を示していますが、2次元解析では面内解析と面外解析でそれぞれ3個ずつ考慮されます。面外解析時の節点の変位は、θX、θY、δZであり、これらは全体座標系での値が使用されます。解析に際しては、モデル全体が剛体移動しないようにするために、地盤などで支えられている節点の3自由度(のすべて、またはどれか)を拘束することになります。
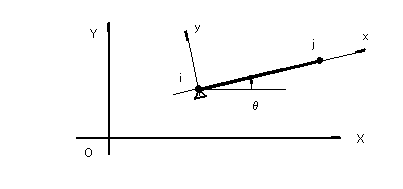
さて、面外解析の支点条件は、一般的には、全体座標系での変位θX、θY、δZを拘束する場合が多いようです。この場合、部材が水平あるいは鉛直に配置されているときは、この支点条件を入力することはそうむずかしいことではありません。ところが、上図のように部材i-jが斜めに配置されている場合はどうでしょうか。 たとえば、i端に設置した支点がこの部材の面外曲げモーメントは伝達するが、ねじりモーメントは伝達しないようにするためには、θX、θY、δZの拘束条件をどのように設定すればよいか、全体座標系で検討している限り、これはかなりむずかしい問題になります。というのは、この部材が水平に配置されていればθYを拘束すれば良いのですが、斜めの場合は、θYの拘束によって、ねじりモーメントも伝達するようになってしまうからです。 しかし、変位の拘束条件を支点座標系で入力できれば、問題は非常に簡単になります。 下図は、全体座標系X-Yに対してθだけ傾いた部材と、i端に設置した支点を示しています。今、支点の傾斜角度としてθを入力し、支点座標系と部材座標系を一致させると、上記の拘束条件はθy(全体座標系でのθYではなく)を拘束するだけで良いことになります。ねじりモーメントを伝達させたいなら、θxを拘束するだけです。
このように、支点の拘束条件を全体座標系ではなく、支点座標系で入力できれば、非常に単純化され、現実の構造から直感的なモデル化が可能になります。本製品で、支点条件として「配置角度」が入力できるようになっているのは、この点も考慮した結果です。
|