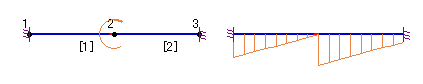|
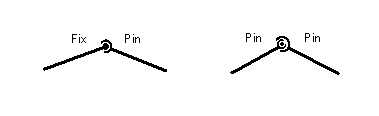
このページでは、解析モデルの作成に役立つ技術情報を掲載しています。 H3: 部材端の結合条件 Frame解析でヒンジ部分をモデル化するときには、一般的に部材端の結合条件をピンにします。これを模式的に表せば下図のようなイメージになります。このとき右の図のように、1つの節点に集まる全部材の結合条件がすべてピンであるとどうなるでしょうか。
Frame解析では、全節点の自由度を未知数とした剛性方程式を解いているので、この節点の回転拘束がまったく無いために回転量が定まらないことが原因して、このままでは解析できません。つまり不安定構造物になってしまいます。これを避けるためには、左の図のように、どれか1つの部材(曲げ剛性が0でない部材)を剛結合にしておくことが確実です。 そうは言っても、トラス橋のようにすべての部材でピンになるようなモデルでは、上記の状況になることが想定できます。そこで本製品では、上図(右)のような節点が入力されたら、剛性方程式を解く直前にこの節点の回転変位を強制的に拘束するようにしています。 その結果、以下のようなことが生じます。 まず両端固定梁の中央にヒンジを設け(部材1のj端をピンにして)、回転モーメント(節点集中荷重)を載荷すると、下図のM図が得られます。
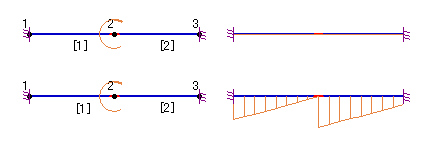
次に部材2のi端側もピンにすると、下図(上)のように曲げモーメントが0という結果になってしまいます。これは強制的に回転を拘束したところへ節点集中荷重が作用しているからです。しかし、荷重種類を部材集中荷重に変えて部材2のi端(載荷位置=0)に載荷すると、下段側の図のように所定のM図が得られます。
実際には、ピンが集まっている節点に回転モーメントを載荷するケースは無いのかもしれませんが、このように入力データによっては内部処理の影響が生じる場合があります。 ヒンジ部にモーメント荷重を載荷するということが何を意味しているか、様々に解釈できる中から確実に意図したような解を得るためには、 最後に、面外解析の場合はどうでしょうか。 面外解析でも同様な処理(同じではない)を行なっていますが、部材が斜めに配置されている場合で材端がピンである位置に固定支点があるとき(1部材のとき)、特に注意が必要です。現行製品ではこのようなデータでも不安定構造物にはなりませんが、正しい解が得られません。この場合は、固定支点を使用するのではなく、ピン支点にして材端条件をFixにすると正しい解が得られます(下図右)。
|